Normal Shocks
The Normal Shock Wave
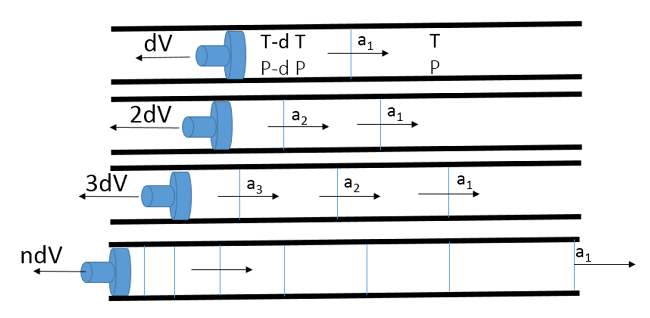
Consider a piston-cylinder layout where the piston is displaced impulsively at a velocity \(dV\).
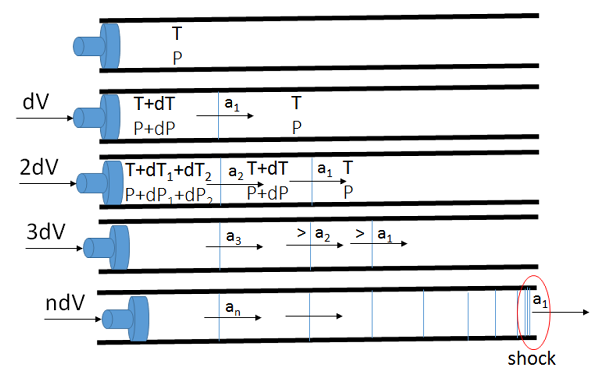
the fluid close to the cylinder must have the same velocity \(dV\) and the disturbance propagates with a sound wave, with a speed \(a1 = \sqrt{\gamma RT}\), where the T is the fluid undisturbed condition. Across the sound, the fluid conditions are different as shown in the pictures \(T + dT1, \, \, P + dP1\).
Now let's assume a second acceleration \(2dV\), the new temperature is \(T + dT1+dT2\) and the pressure is \(P +dP1+dP2\). The second wave is travelling faster than the rest one because \(a2 = \sqrt{R(T + dT )}\). It is clear that the second wave will reach the rest one but it cannot overtake it. The process can be repeated with other accelerations of the piston but all the waves will merge with the rest one. This front of coalescence of pressure waves is a shock.
A shock wave is a region of very rapid flow changes, whose width is usually measured as a few mean free paths (average distance between molecular collisions, or order \(6.7 \times 10^{-5}\) mm in air at sea level conditions). The internal structure of the shock wave is therefore only modelled correctly by statistical methods based upon the kinetic theory of gases. All our aerodynamics is continuum aerodynamics, where the thermodynamic properties result from molecular behaviour but where we never `see' individual molecules however small we might make our `control volume' or computational cell.
At sea level, the thickness of a shock wave is therefore negligible compared, say, with the chord of a wing. We, therefore, treat the shock wave as if it truly were a discontinuity. At high altitude - 60 Km plus - then the mean free path becomes so large that shock thicknesses may be larger than the body itself. Such flows have to be modelled by techniques that are molecular in nature.
The classical analysis for a shock wave considers the process as inviscid, although viscous stresses within the shock wave are probably larger than for any possible boundary layer flow. It achieves this by taking a control volume around it that is sufficiently far from the shock wave that the viscous stresses can be regarded as negligible. The analysis correctly then predicts the `jump' or `transition' across the shock wave but cannot model the internal structure.
The idea of the piston can be used to show that the expansion due to the piston leads to a dispersion of the waves, not to a coalescence (expansion waves)
Consider a shock wave moving at speed \(U_s\) into a gas (strictly any medium) at state 1. It induces conditions at state 2 behind it.
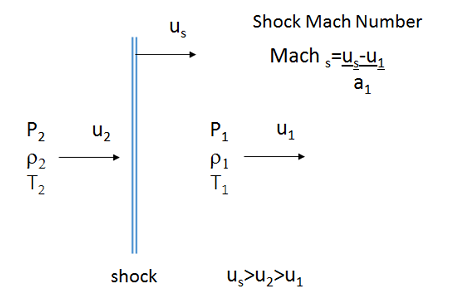
If, as observers, we also move at speed Us then we reduce the shock to rest. This is the most convenient framework for analysis (frame of reference: shock at rest)
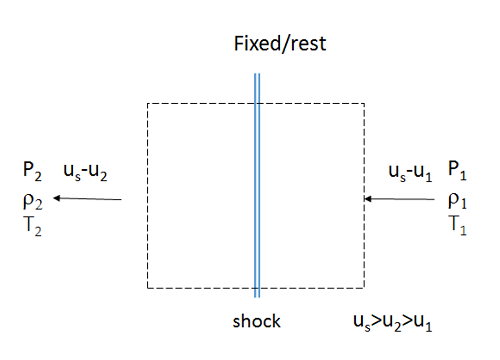
mass: \( \rho_1(U_s - u _1 ) = \rho_2 (U_s - u_2 ) \)
\(x\)-momentum: \( p_1 + \rho_(U_s - u_1)^2 = p_2 + \rho_2(U_s - u_2 )^2 \)
Eliminating \( (U_s - u_1 ) \) and rearranging gives
\[ ( U_s - u_1 ) = \sqrt{\frac{(p_2-p_1)\rho_2}{\rho_1(\rho_2-\rho_1)}}. \]
Note that we have made no mention of an equation of state so that this result applies to any substance; the only assumption has been that the ow can be transformed to a steady frame of reference by the addition of constant velocity.
If the wave is very weak(i.e the gradients of velocity and temperature can be neglected) then the following approximation is valid: \( U_s-u_1 \approx \sqrt{\frac{\partial p}{\partial \rho}} .\)
In a very weak wave, internal friction and heat transfer are negligible and the motion can e assumed isentropic. Thus \( ( a^2 = \left( \frac{\partial p}{\partial \rho}\right)_S \) where \(a \) is the speed of sound, the speed at which a very weak pressure wave propagates relative to the gas.